n alatt a k | ismétlés nélküli kombinációszámítás magyarázat

#HogyIsVanEz Mi az és hogy kell kombinációt számítani? Mi az az n alatt a k? Nézzük meg! – Példákkal és magyarázattal!

A kombináció számítással, azaz az n alatt a k-val azt lehet kiszámolni, hogy hányféleképpen tudunk k dolgot kiválasztani n-ből. Itt most a képlet „sorrend nem számít, ismétlés nélkül” kategóriáját vizsgáljuk.

Nézzünk meg egy példát! Egy hat fős társaságban mindenki mindenkivel (önmagán kívül) kezet fog, hány kézfogás történik? Ezt lehetne úgy is, hogy 4+3+2+1, mivel először az első ember a másik 4-tel fog kezet, utána ő kiesik, jön a második, aki már csak 3-mal fog kezet, és így tovább, egészen addig, amíg az utolsó kézfogás meg nem történik. Ám ha azt mondom számítsd ki, hogy ha egy 1000 fős társaságban mindenki mindenkivel kezet fog, hány kézfogás történik, egy cseppet bajban lennél, mert ha még számológéppel is, elég sok idő lenne leírni a műveletet, hogy 999+998+997+[...]+1. De nem kell aggódni, van egy egyszerűbb megoldás!

...Ami a következő:

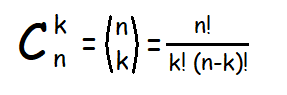
...bár lehet, hogy első ránézésre bonyolultabb... remélem rájövünk, hogy ennek pontosan az ellentéte az igaz...

A képlet: n faktoriálisban a ( (k faktoriális szer az n-k faktoriális) ).

Ugye a faktoriálissal is egyfajta kombinációt lehet számolni, annak a módszere, hogy n*(n-1)*(n-2)*(n-3)*[...]*1. Jele: !.

Szóval így például 5 faktoriális (ami egyébként 120) 5*4*3*2*1. Ha kiszámoljuk a képletet a példánkkal (akár számológéppel) akkor ->

1. n = 5 - az n jelenti az összeset; k = 2 - ez jelenti a kiválasztást, minden alkalommal 2 ember fog kezet, két főt választunk ki.

2. n! = 120; k!*(n-k)! = 2*(5-2)! = 2*3! = 2*6 = 12

3. n! = 120; k!*(n-k)! = 12;

4. 120 / 12 = 10

5. KÉSZ! Az eredmény 10.

És ha leellenőrizzük kicsit bonyolultabban: 4+3+2+1=10 - Hurrá! Vagyis tényleg működik! Így ha azt akarjuk kiszámolni, hogy ha egy 1000 fős társaságban mindenki mindenkivel kezet fog, hány kézfogás történik, akkor számológéppel kiszámolva: 499 500. A tudományos számológépeken általában nCr gombbal szokták jelölni.

Ha többet meg szeretnél tudni a képletről vagy esetleg gyakorolnád a használatát érdemes felkeresni a következő oldalakat:

Matek4u: kombináció;

Wikipédia: binomiális együttható;

ZseniLeszek: n alatt a k;